После записи условия учащиеся должны себе представить физический процесс, о котором идет речь в задаче, и, если это требуется, присоединить к данным в задаче величинам другие, взятые из таблиц. После того как выписаны все данные, столбец подчеркивают и под чертой подписывают искомые величины со знаком вопроса. Например, задачу «Стальную деталь массой 30 кг нагревают от 20 до 1120°С. Какое количество теплоты необходимо для нагревания?» записывают так:
Дано:
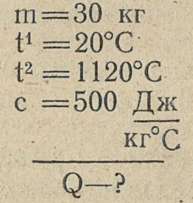
Затем учащиеся должны обратить внимание, в одной ли системе единиц выражены все данные. Последнее замечание раньше распространялось обычно только на старшие классы, теперь же, когда Международная система единиц введена в школьное преподавание уже с VI класса, следует обратить на эту сторону решения задачи должное внимание, не употребляя слова «система единиц» (они не упоминаются в учебниках VI и VII классов).
Выполнив все это, приступают к решению задачи, причем на первой ступени обучения физике допустимо проводить решение по отдельным действиям, не делая его сначала в общем виде; на второй ступени рекомендуется дать сначала решение в общем виде, то есть в буквенных обозначениях, а затем, подставив числовые значения величин с их обозначениями, вычислить значение искомой величины.
Очень важно, чтобы на второй ступени обучения выполнялись методические указания к решению задач по отдельным, разделам курса физики.
В VIII классе при изучении механики большое внимание современная методика физики уделяет основной задаче, механики — определению положения тела в любой момент времени по заданным начальным условиям (начальные координаты и скорость) и действующим на тело силам. В решении задач используется координатный метод и идеи относительности движения.
Решение любой задачи по кинематике начинают с выяснения того, движение каких тел описано в задаче и какое тело следует выбрать в качестве, тела отсчета. О телом отсчета связывают систему координат и на рисунке показывают выбранное положительное направление координатных осей. Обращают внимание на начальные условия: для этого такие величины, как начальная координата, начальная скорость и ускорение, указывают на чертеже. Затем составляют уравнение или систему уравнений для координаты, перемещения или скорости в зависимости от условий задачи; проверяют, достаточно ли полно и правильно составлена система уравнений, и, решая ее в общем виде, получают расчетную формулу для неизвестной величины. Затем подставляют в эту формулу данные значения величин, выраженные в одной системе, и производят расчет.
В заключение следует проверить правильность полученного ответа (реальность результата, правильность наименований).
При решении задач по динамике вначале также выбирают тело отсчета и связанную с ним систему координат, которую изображают па чертеже. Затем следует выявить все силы, действующие на тело, движение которого рассматривается в задаче. Для этого нужно установить, с какими телами взаимодействует данное тело и какова природа каждого взаимодействия (тяготение, упругая деформация, трение). Все действующие силы обозначают на чертеже. Затем записывают для данного тела уравнение второго закона Ньютона (если в задаче рассматривается система тел, то уравнение записывают для каждого тела) в векторной форме, а для перехода к скалярной форме записи уравнений все векторы проектируют на координатные оси. Проверяют, соответствует ли число уравнений числу неизвестных, и решают задачу сначала в общем виде, а затем с числовыми данными.
В VIII—X классах большое внимание уделяется графическим задачам. Например, в механике по графику зависимости скорости тела от времени определяют ускорение, действующую на тело силу (указывая, чему равна масса тела); в IX классе при изучении тепловых явлений очень полезны задачи на построение графиков зависимости между параметрами идеального газа — его давлением, температурой, объемом, а также задачи, в которых по графику процесса изменения состояния идеального газа в одних координатах нужно, представить процесс в других координатах (например, данный график изменения состояния идеального газа в координатах давления Р и температуры Т представить в координатах объема V и температуры).
Разработан ряд рекомендаций по подбору, содержанию, методике решения задач. Например, при подборе задач с техническим содержанием, без которых, Конечно, невозможен учебный процесс по физике, следует выполнять определенные требования: содержание задачи должно быть тесно связано с изучаемым программным материалом, в ней должны быть использованы реальные данные, поставлены вопросы, действительно встречающиеся в практике; желательно использовать при решении таких задач техническую документацию, рассматривать наиболее распространенные технические объекты и процессы. Используются данные пятилетних планов, достижения отечественной техники.
Чтобы задачи играли развивающую роль, в их решении должна максимально проявляться самостоятельность учащихся. Не следует объяснять на уроках решение почти каждой конкретной задачи, нужно лишь показать на нескольких примерах приемы записи и анализа типовых задач.
Для самых сильных учащихся рекомендуется систематически подбирать одну сложную задачу, указывая в домашнем задании, что ее решение не обязательно для всех (например, заключай номер этой задачи в скобки).
Самостоятельность в решении задач вырабатывается систематической и тщательной проверкой их выполнения. При проверке нужно требовать анализа и понимания решения задач, кратко указывать ошибки в их записи и решении. При выставлении оценки за четверть следует учитывать качество выполнения задач (для удобства учитель может в специальной тетради, в отведенной графе, записывать оценки выполнения домашнего задания). Полезно записывать в ученических тетрадях для домашних заданий краткие индивидуальные советы, по устранению ошибок, номера задач, которые должен решить ученик, чтобы ликвидировать пробелы в своих знаниях. Для облегчения проверки можно применять программированные задания.